- 详情
- 信息
- 推荐
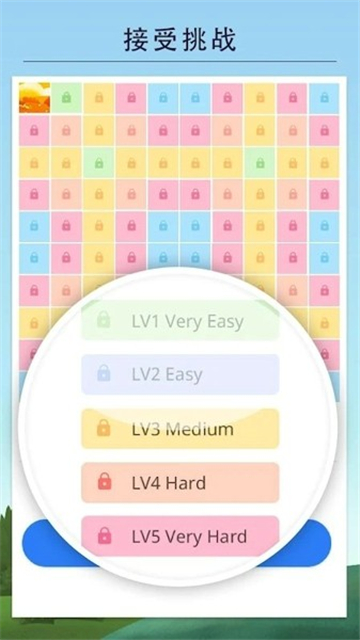
nonogram安卓版是一款玩起来非常烧脑的解谜游戏,在nonogram安卓版游戏中,玩家需要通过数字提示在方格中涂色,最终呈现出一幅精美的像素图画。从简单的9x9方格到复杂的25x25挑战,数百个精心设计的关卡让你享受循序渐进的烧脑体验哦,每完成一幅作品,都能获得满满的成就感,看着黑白数字逐步变成生动的图案非常的带感哦。
nonogram安卓版怎么玩?
本系列中的简称及其说明
1、排:行/列
2、垂直:与排的方向垂直。
3、从k排开始的m×n区块:未特指时,通常指游戏中的所有排的集合。也可以表示一个矩形的范围,其中,m表示行,n表示列。
4、场地格:初始状态的格子,存在在游戏的区块中。
5、第x行格:从任意一边开始数的第x个场地格
6、第x个数字:从任意一边开始数第x个数字
7、数字x的正格:一定有黑块的格子,且该场地格一定为数字x的图形的一部分
8、负格:一定无黑块的格子
9、数字x的位:数字x所可能代表的场地格
第一章:数字的位与数字的位的确定化
1-1概述
在数织的过程中,我们就是在与一些模糊的位置打交道,通过这些位置还有区块相互间的关系,我们可以将他们中一部分的准确位置确定,最终成功推演出整个图像。
数字的准确位置一般可以由一排的格数和数字推出,有时也需要用到已经确定的正格与负格,只有极少数的关卡需要同时用到两排以上的信息。这也使得其的难度不是那么的高,本系列致力于帮您从刚入门的新手迅速成为能推理大多数图形的高玩。
注:以下所有定理与方法中我们将把负数看为零。
1-2 推演基础
如何才能通过推演确定准确位置?我们可以先提出一条十分简单的定理。
若一排有且仅有一个数字,则这个不是数字的位的场地格均为负格。(1-2-1)
这条定理不证自明,也可以说是数字的位定义的另一种表达。
由这条公理,我们可以看出,确定一个数字的准确位置,就是使其的位减少到无法再减少为止。而交叉的排与单排的限制可以帮助我们减少数字的位。
我们来看一个简单的例子。
图1-2-1
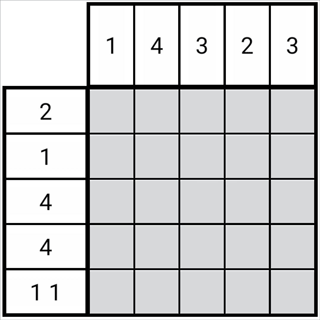
如图所示,每一排的黑块在规则下都有有限种分布情况,这些分布情况称为分布可能。
图中第二列共有两种分布可能,而两种分布可能中有一些公共部分,可以看出,这个公共部分中的格子一定是正格。
同理,图中第三列共有三种分布可能,这三种分布可能中也有公共部分,即第三列第三格。于是这个格子一定也为正格。
更一般的,在一排的所有分布可能中,恒有黑块的格子为正格。
如果一个排有一个正格且只有一个数字,我们可以把他看做“固定住”这个数字的位的“钉子”,而位可以在其左右“波动”,或者说增加格数,从而得出所有的分布可能。
同时,当有两个正格固定住一个数字的位时,其中间的部分也就确定下来一定是正格了。我们也可以用数学的语言来将其转换为如下表述:
若一排有且仅有一个数字,且确定了第m行格与第n行格均为正格,则第i行格为正格。其中,i∈{x∈N+|m≤x≤n或n≤x≤m}。(1-2-2)
然而,因为数字的大小关系,一个数字的位在正格的两边增加一定数量的格数。不能超过数字所规定的范围,我们从数学角度对其进行推导。
设一排有且仅有一个数字k,第m行格与第n行格为已知正格,且m≧n。由式1-2-2,可知其中间所有格均为正格,总共占去(m-n+1)格。于是,位在左右能增加的格数为k-(m-n+1)。所以,从两端增加这么多的格数即可得到所有的位。既,从第n-[k-(m-n+1)]行格到第m+[k-(m-n+1)]都为该数字的位。整理后可得:
若一排有且仅有一个数字k,且第m行格和第n行格都为正格,则该数字的位为第(-k+m+1)行格到第(k+n-1)行格。(m≧n)(1-2-2)
1-3边缘法
我们在上面提到,数字能够限制位,其实,还有一种东西能够限制位。那就是场地格的边缘。场地格的边缘以外显然不能存在位,尤其是第一个数字,其必然最接近场地格的边缘,所以很容易被限制。所以,我们有必要讨论边缘的情况。
图1-3-1
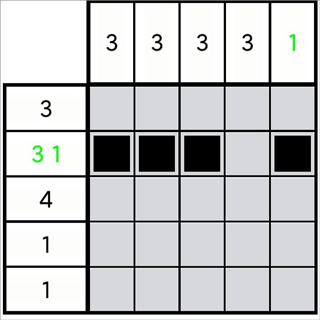
如图1-3-1,显然,图中第1列的位不能向上增加两格,然而其确实满足定理(1-2-3)的前置条件。我们可以换一种思考方式,如果不能向上增加,则一定要向下增加。因此,向上不能增加多少格,向下就要增加多少格。
设一排有且仅有一个数字m,且已知第n行格为正格,其中m>n。则其无法增加的格数为(m-n)格。将这些格数向下增加,则可以得到:
若一排有且仅有一个数字m,且第n行格为正格,m>n,则第i行格为正格,i∈[n,m],i∈N+。(1-3-1)
观察该定理,当m>n时,就意味这该数字代表的位一定覆盖了第1行格到第n行格。如果我们假设其为第一个数字,那么可以想到,这个定理依然成立。于是有:
若一排第n行格为正格,且第一个数字为m,则第i行格为正格,其中,i∈[n,m],i∈N+。(m>n)(1-3-2)
当一个数字在边缘时,其状态并没有太多的变化,但是,如果我们讨论一整排的情况,又会如何?
这里我们引入一种方法:整体法,当确定两个相邻数字的位时,我们可将这两个数字当看做一个数字处理,他们的位看做这个数字的位。这种处理方法可以简化我们的运算以及帮助我们分析一整排的情况。
我们可以注意到一个事实——多个数字组成的整体处在边缘处时有种独特的分布——数字-空格-数字-空格。这种分布把数字占用的空间压缩为了最小,我们把这种整体在边缘的分布称为边缘状态。
如果一个实心物体在一条直道内滑动,可以想象,其投影与初始时投影公共部分的大小将不断减少,因此,公共部分其所有运动瞬间投影的公共部分与其边缘状态的公共部分相同。由此,我们可以得出:
没有负格的一排的所有分布可能的公共部分由其边缘状态决定。
可以看出,这种描述看似十分完美,实际上有一点瑕疵,那就是作为一个整体,多个数字占用的空间可以拉长和缩短,而边缘状态一定是最短的。但确实,我们就差一步就能完善它了。
图1-3-2
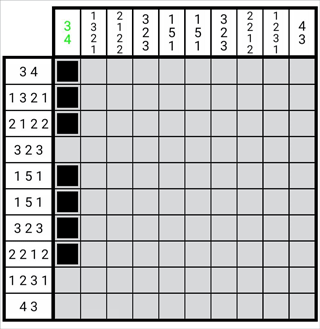
如图,我们可以在第一列从上向下构造一个图形,其为第一列所有数字整体的边缘状态,这时,这一列从下向上数共有2个空格。这意味着这个图形每个数字的位都可以向下增加两格,于是我们将图形中对应每个数字的图形从上至下减去两格,如图所示。
图1-3-3
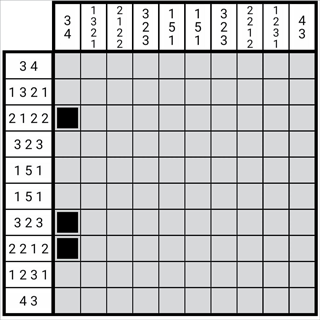
这样我们就得到了这一列的正格。这种方法得出的最终图形是与原来图形的数字位相对应的。这里我们省略了边缘状态的检查。边缘状态的重叠不重要,重要的数字与图形必须一一对应。因为这个图形可以变长变短,但是其中任意一个图形活动的范围是有限的,其限制正好就是他自身与区块的长度。只有当图形与数字一一对应时这种方法才有意义。由此,我们也反推出了为何其必然一一对应,也可以将该性质运用在解题中。这也是为第二章的一些铺垫。
图1-3-4
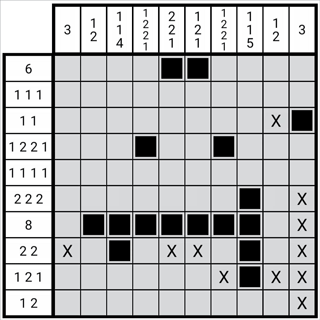
如图,图中第七列第七行为用此方法确定的第七列第3个数字2,由于位置关系的对应,第4个数字1的位一定是第七列第十行。
由上,我们可以总结一种快速的确定正格的方法:先从一排从第一行格按顺序做出如上的数字-空格图形,再从开始的方向减去最后剩下的空格数,将负数看为零。最后得到的图形一定为正格。同时这些图形也与原来图形中的位置关系相对应,也是运用第一章所有方法所能得到的最多正格,这种方法被称为边缘法。
游戏玩法
■5种挑战模式。选择最适合您的数织游戏难度等级。
■多种主题拼图等待您去挑战。不要忘了领取成就奖励。
■轻松愉快的背景音乐,能使自己快速放松下来
■发现新的拼图。解锁越来越多的新世界。
游戏说明
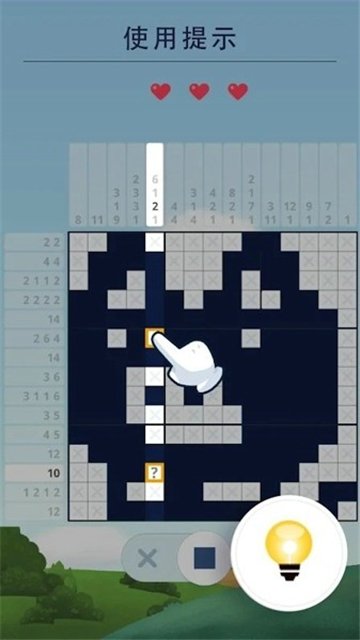
这款游戏基于数织的玩法开发并且加入了提示功能。
不过它也有缺点,就是不能真正提示答案,只能根据你当前拼出的图案给出下一步的提示。
所以当玩那些很大的图案的时候一旦眼花拼错一个就会满盘皆错。
游戏评测
nonogram安卓版是一款非常有挑战性的解谜闯关游戏,在nonogram安卓版游戏中,每日挑战和成就系统让玩家保持新鲜感,适合碎片时间游玩。如果你喜欢逻辑推理或像素艺术,这款游戏绝对适合你!
- 当前版本1.6.9
- 系统要求需要支持安卓系统5.2以上
- 是否收费免费(游戏内购买项目)
- 游戏语言中文
- 包名nonogram.logicpuzzles.picturecross.pixel
- MD5f1eda75db9509692c22fefcc8834ac10
- 权限点击查看
- 隐私说明查看详情